<div data-elementor-type="wp-post" data-elementor-id="8856" class="elementor elementor-8856">
				<div class="elementor-element elementor-element-0ec4e31 e-flex e-con-boxed e-con e-parent" data-id="0ec4e31" data-element_type="container">
					<div class="e-con-inner">
				<div class="elementor-element elementor-element-2825f35 elementor-widget elementor-widget-text-editor" data-id="2825f35" data-element_type="widget" data-widget_type="text-editor.default">
				<div class="elementor-widget-container">
									<div class="dad65929">
<div class="_4f9bf79 d7dc56a8 _43c05b5">
<div class="ds-message _656c965">
<div class="ds-markdown">
<p class="ds-markdown-paragraph">Les semelles de fondation sont des éléments structurels essentiels qui transmettent les charges d’un ouvrage au sol. Elles doivent être conçues avec précision pour garantir la stabilité et la durabilité de la construction. On distingue principalement deux types de semelles : les semelles <strong>isolées</strong> (ou ponctuelles) et les semelles <strong>filantes</strong> (ou continues). Cet article détaille les méthodes de calcul selon les normes BAEL 91 révisées 99 et propose un outil Excel pour simplifier la conception.</p>
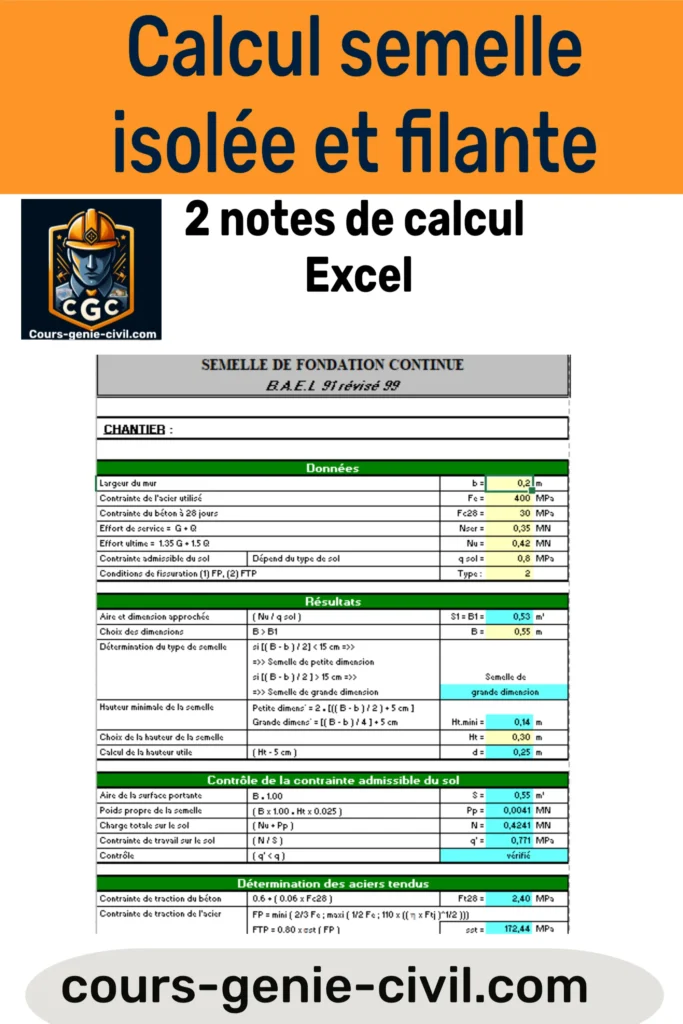
<p><img class="image_Feuille_Excel_calcul_semelle_isolée_semelle_filante alignnone wp-image-8859 size-large" title="Feuille Excel de calcul pour semelle isolée et semelle filante avec données techniques et résultats automatisés" src="https://cours-genie-civil.com/wp-content/uploads/2025/09/2-Notes-de-Calcul-de-Semelle-isolee-et-semelle-filante-sur-Feuille-Excel-683x1024.webp" alt="Schéma technique illustrant les calculs de semelle isolée et semelle filante sur feuille Excel, avec annotations de charges et dimensions." width="683" height="1024" /></p>
<hr />
<h2>Partie 1 : La Semelle Isolée (Ponctuelle)</h2>
<h3>1.1 Définition et Cas d’Usage</h3>
<p class="ds-markdown-paragraph">Une semelle isolée est utilisée pour supporter un poteau unique. Elle répartit la charge sur une surface suffisante pour ne pas dépasser la contrainte admissible du sol.</p>
<h3>1.2 Données de Calcul</h3>
<ul>
<li>
<p class="ds-markdown-paragraph">Dimensions du poteau : <span class="katex"><span class="katex-mathml">a=0,25 m</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">a</span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">25</span><span class="mord mathnormal">m</span></span></span></span>, <span class="katex"><span class="katex-mathml">b=0,30 m</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">b</span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">30</span><span class="mord mathnormal">m</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Charges : <span class="katex"><span class="katex-mathml">Nser=0,4 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">N</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ser</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">4</span><span class="mord mathnormal">MN</span></span></span></span>, <span class="katex"><span class="katex-mathml">Nu=0,6 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">N</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">u</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">6</span><span class="mord mathnormal">MN</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Contraintes : <span class="katex"><span class="katex-mathml">σsol=0,42 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">so</span><span class="mord mathnormal mtight">l</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">42</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span>, <span class="katex"><span class="katex-mathml">fc28=35 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">f</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">c</span>28</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">35</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span>, <span class="katex"><span class="katex-mathml">fe=500 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">f</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">e</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">500</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Type de fissuration : FP (peu préjudiciable)</p>
</li>
</ul>
<h3>1.3 Calcul des Dimensions</h3>
<p class="ds-markdown-paragraph">La surface approximative est donnée par :</p>
<p><span class="katex-display ds-markdown-math"><span class="katex"><span class="katex-mathml">S1=Nuσsol=0,60,42=1,43 m2</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">S</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">so</span><span class="mord mathnormal mtight">l</span></span></span><span class="vlist-s">​</span></span><span class="mord mathnormal">N</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">u</span></span><span class="vlist-s">​</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist">0<span class="mpunct">,</span>420<span class="mpunct">,</span>6</span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">1</span><span class="mpunct">,</span><span class="mord">43</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></p>
<p class="ds-markdown-paragraph">Avec un débord constant, on obtient :</p>
<p><span class="katex-display ds-markdown-math"><span class="katex"><span class="katex-mathml">A=1,20 m,B=1,25 m</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">A</span><span class="mrel">=</span></span><span class="base"><span class="mord">1</span><span class="mpunct">,</span><span class="mord">20</span><span class="mord mathnormal">m</span><span class="mpunct">,</span><span class="mord mathnormal">B</span><span class="mrel">=</span></span><span class="base"><span class="mord">1</span><span class="mpunct">,</span><span class="mord">25</span><span class="mord mathnormal">m</span></span></span></span></span></p>
<h3>1.4 Vérification de la Contrainte au Sol</h3>
<ul>
<li>
<p class="ds-markdown-paragraph">Surface réelle : <span class="katex"><span class="katex-mathml">S=A×B=1,50 m2</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">S</span><span class="mrel">=</span></span><span class="base"><span class="mord mathnormal">A</span><span class="mbin">×</span></span><span class="base"><span class="mord mathnormal">B</span><span class="mrel">=</span></span><span class="base"><span class="mord">1</span><span class="mpunct">,</span><span class="mord">50</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Poids propre : <span class="katex"><span class="katex-mathml">Pp=0,0113 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">P</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">p</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">0113</span><span class="mord mathnormal">MN</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Charge totale : <span class="katex"><span class="katex-mathml">N=0,6113 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">N</span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">6113</span><span class="mord mathnormal">MN</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Contrainte effective : <span class="katex"><span class="katex-mathml">σ′=NS=0,408 MPa<;σsol</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">′</span></span></span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">S</span></span></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">N</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">408</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span><span class="mrel"><;</span></span><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">so</span><span class="mord mathnormal mtight">l</span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span> â </p>
</li>
</ul>
<h3>1.5 Calcul des Aciers</h3>
<ul>
<li>
<p class="ds-markdown-paragraph">Contrainte admissible de l’acier : <span class="katex"><span class="katex-mathml">σst=250 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">s</span><span class="mord mathnormal mtight">t</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">250</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Section d’acier longitudinal :</p>
</li>
</ul>
<p><span class="katex-display ds-markdown-math"><span class="katex"><span class="katex-mathml">Ax=Nser8⋅B−bd⋅σst=7,60 cm2</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">x</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist">8<span class="mord mathnormal">N</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ser</span></span></span><span class="vlist-s">​</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mbin">⋅</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="mord mathnormal">d</span><span class="mbin">⋅</span><span class="mord mathnormal">σ</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">s</span><span class="mord mathnormal mtight">t</span></span></span><span class="vlist-s">​</span></span><span class="mord mathnormal">B</span><span class="mbin">−</span><span class="mord mathnormal">b</span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">7</span><span class="mpunct">,</span><span class="mord">60</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></p>
<ul>
<li>
<p class="ds-markdown-paragraph">Section d’acier transversal :</p>
</li>
</ul>
<p><span class="katex-display ds-markdown-math"><span class="katex"><span class="katex-mathml">Ay=Nser8⋅A−ad⋅σst=7,60 cm2</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">y</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist">8<span class="mord mathnormal">N</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ser</span></span></span><span class="vlist-s">​</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mbin">⋅</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="mord mathnormal">d</span><span class="mbin">⋅</span><span class="mord mathnormal">σ</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">s</span><span class="mord mathnormal mtight">t</span></span></span><span class="vlist-s">​</span></span><span class="mord mathnormal">A</span><span class="mbin">−</span><span class="mord mathnormal">a</span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">7</span><span class="mpunct">,</span><span class="mord">60</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></p>
<hr />
<h2>Partie 2 : La Semelle Continue (Linéaire)</h2>
<h3>2.1 Définition et Applications</h3>
<p class="ds-markdown-paragraph">Une semelle continue supporte un mur ou une série de charges linéaires. Elle est utilisée lorsque les charges sont réparties sur une longueur importante.</p>
<h3>2.2 Données de Calcul</h3>
<ul>
<li>
<p class="ds-markdown-paragraph">Largeur du mur : <span class="katex"><span class="katex-mathml">b=0,20 m</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">b</span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">20</span><span class="mord mathnormal">m</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Charges : <span class="katex"><span class="katex-mathml">Nser=0,35 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">N</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ser</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">35</span><span class="mord mathnormal">MN</span></span></span></span>, <span class="katex"><span class="katex-mathml">Nu=0,42 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">N</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">u</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">42</span><span class="mord mathnormal">MN</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Contraintes : <span class="katex"><span class="katex-mathml">σsol=0,80 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">so</span><span class="mord mathnormal mtight">l</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">80</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span>, <span class="katex"><span class="katex-mathml">fc28=30 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">f</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">c</span>28</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">30</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span>, <span class="katex"><span class="katex-mathml">fe=400 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">f</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">e</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">400</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Type de fissuration : FTP (très préjudiciable)</p>
</li>
</ul>
<h3>2.3 Calcul des Dimensions</h3>
<ul>
<li>
<p class="ds-markdown-paragraph">Largeur approximative :</p>
</li>
</ul>
<p><span class="katex-display ds-markdown-math"><span class="katex"><span class="katex-mathml">B1=Nuσsol=0,53 m⇒B=0,55 m</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">B</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">so</span><span class="mord mathnormal mtight">l</span></span></span><span class="vlist-s">​</span></span><span class="mord mathnormal">N</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">u</span></span><span class="vlist-s">​</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">53</span><span class="mord mathnormal">m</span><span class="mrel">⇒</span></span><span class="base"><span class="mord mathnormal">B</span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">55</span><span class="mord mathnormal">m</span></span></span></span></span></p>
<h3>2.4 Vérification de la Contrainte au Sol</h3>
<ul>
<li>
<p class="ds-markdown-paragraph">Surface : <span class="katex"><span class="katex-mathml">S=B×1,00=0,55 m2</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">S</span><span class="mrel">=</span></span><span class="base"><span class="mord mathnormal">B</span><span class="mbin">×</span></span><span class="base"><span class="mord">1</span><span class="mpunct">,</span><span class="mord">00</span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">55</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Poids propre : <span class="katex"><span class="katex-mathml">Pp=0,0041 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">P</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">p</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">0041</span><span class="mord mathnormal">MN</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Charge totale : <span class="katex"><span class="katex-mathml">N=0,4241 MN</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">N</span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">4241</span><span class="mord mathnormal">MN</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Contrainte effective : <span class="katex"><span class="katex-mathml">σ′=0,771 MPa<;σsol</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">′</span></span></span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">0</span><span class="mpunct">,</span><span class="mord">771</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span><span class="mrel"><;</span></span><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">so</span><span class="mord mathnormal mtight">l</span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span> â </p>
</li>
</ul>
<h3>2.5 Calcul des Aciers</h3>
<ul>
<li>
<p class="ds-markdown-paragraph">Contrainte admissible de l’acier : <span class="katex"><span class="katex-mathml">σst=172,44 MPa</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">σ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">s</span><span class="mord mathnormal mtight">t</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">172</span><span class="mpunct">,</span><span class="mord">44</span><span class="mord mathnormal">MP</span><span class="mord mathnormal">a</span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Section d’acier minimal : <span class="katex"><span class="katex-mathml">Ax,min=2,00 cm2</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">x</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight">min</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">2</span><span class="mpunct">,</span><span class="mord">00</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></p>
</li>
<li>
<p class="ds-markdown-paragraph">Section d’acier longitudinal :</p>
</li>
</ul>
<p><span class="katex-display ds-markdown-math"><span class="katex"><span class="katex-mathml">Ay=Nser8⋅B−bd⋅σst=3,55 cm2/ml</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">y</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist">8<span class="mord mathnormal">N</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ser</span></span></span><span class="vlist-s">​</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mbin">⋅</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="mord mathnormal">d</span><span class="mbin">⋅</span><span class="mord mathnormal">σ</span><span class="msupsub"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">s</span><span class="mord mathnormal mtight">t</span></span></span><span class="vlist-s">​</span></span><span class="mord mathnormal">B</span><span class="mbin">−</span><span class="mord mathnormal">b</span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">3</span><span class="mpunct">,</span><span class="mord">55</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span><span class="mord">/</span><span class="mord mathnormal">m</span><span class="mord mathnormal">l</span></span></span></span></span></p>
<ul>
<li>
<p class="ds-markdown-paragraph">Section d’acier transversal : <span class="katex"><span class="katex-mathml">Ax=max⁡(Ay4;Ax,min)=2,00 cm2</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">x</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mop">max</span><span class="minner"><span class="mopen delimcenter"><span class="delimsizing size2">(</span></span><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">A</span><span class="msupsub"><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">y</span></span><span class="vlist-s">​</span></span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mpunct">;</span><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">x</span><span class="mpunct mtight">,</span><span class="mord mathnormal mtight">min</span></span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mclose delimcenter"><span class="delimsizing size2">)</span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">2</span><span class="mpunct">,</span><span class="mord">00</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal">m</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></p>
</li>
</ul>
<hr />
<h2>Partie 3 : Feuille de Calcul Excel pour Semelles</h2>
<p class="ds-markdown-paragraph">Pour faciliter le dimensionnement, nous mettons à disposition un fichier Excel automatisé incluant :</p>
<ul>
<li>
<p class="ds-markdown-paragraph">Calcul automatique des dimensions et des sections d’acier</p>
</li>
<li>
<p class="ds-markdown-paragraph">Vérification de la contrainte au sol</p>
</li>
<li>
<p class="ds-markdown-paragraph">Adaptation aux normes BAEL 91 révisées 99</p>
</li>
</ul>
<h4>Téléchargement du Fichier Excel</h4>
<p class="ds-markdown-paragraph"><span style="font-size: 2em;">ð <b data-original-attrs="{";style";:";";}">ððð</b> <strong><a href="https://cours-genie-civil.com/wp-content/uploads/2025/09/semelle-de-fondation.xls">[Lien de téléchargement]</a></strong></span></p>
<p><em>Description : Cet outil permet de concevoir rapidement des semelles isolées et continues en suivant les normes en vigueur.</em></p>
<h2>Chapitre des liens utiles</h2>
<p>Voici une sélection de ressources essentielles pour le génie civil, couvrant les fondations et la mécanique des sols.</p>
<hr />
<p><b>Calcul et dimensionnement de fondations</b></p>
<p>Apprenez à effectuer le <b><a class="ng-star-inserted" href="https://cours-genie-civil.com/calcul-et-dimensionnement-dune-semelle-filante-guide-pratique-pdf/" target="_blank" rel="noopener" data-hveid="0" data-ved="0CAAQ_4QMahcKEwiJkfuV_L6PAxUAAAAAHQAAAAAQWg">calcul et le dimensionnement d&rsquo;une semelle filante</a></b> avec ce guide pratique en PDF. Ce document détaillé vous expliquera les étapes cruciales, du pré-dimensionnement au ferraillage, en intégrant les vérifications sismiques pour une conception solide et conforme. Pour approfondir vos connaissances, ce cours complet sur les <b><a class="ng-star-inserted" href="https://cours-genie-civil.com/comprendre-les-fondations-superficielles-cours-pdf-a-telecarger/" target="_blank" rel="noopener" data-hveid="0" data-ved="0CAAQ_4QMahcKEwiJkfuV_L6PAxUAAAAAHQAAAAAQWw">fondations superficielles</a></b> vous aide à comprendre les principes de conception et le comportement des sols sous charge.</p>
<hr />
<p><b>Travaux pratiques et exercices</b></p>
<p>Mettez en pratique vos compétences en mécanique des sols et en fondations superficielles grâce à des <b><a class="ng-star-inserted" href="https://cours-genie-civil.com/td-exercices-corriges-mecanique-des-sols-et-fondations-superficielles/" target="_blank" rel="noopener" data-hveid="0" data-ved="0CAAQ_4QMahcKEwiJkfuV_L6PAxUAAAAAHQAAAAAQXA">exercices corrigés en PDF</a></b>. Ces travaux dirigés sont conçus pour vous aider à maîtriser l&rsquo;application des concepts théoriques, incluant des exemples sur le calcul de la capacité portante.</p>
<hr />
<p><b>Outils de calcul sur Excel</b></p>
<p>Simplifiez vos projets de calcul avec des outils pratiques. Cette <b><a class="ng-star-inserted" href="https://www.4geniecivil.com/2023/01/feuille-excel-de-calcul-de-semelle.html" target="_blank" rel="noopener" data-hveid="0" data-ved="0CAAQ_4QMahcKEwiJkfuV_L6PAxUAAAAAHQAAAAAQXQ">feuille Excel de calcul de semelle</a></b> est un modèle qui facilite le dimensionnement et le ferraillage des semelles sous deux poteaux. Vous trouverez également des <b><a class="ng-star-inserted" href="https://www.4geniecivil.com/2018/05/calcul-de-semelles-sur-excel.html" target="_blank" rel="noopener" data-hveid="0" data-ved="0CAAQ_4QMahcKEwiJkfuV_L6PAxUAAAAAHQAAAAAQXg">modèles de calcul sur Excel</a></b> pour différents types de fondations, y compris les semelles isolées, filantes, les murs de soutènement et les radiers.</p>
<hr />
<p><b>Normes de calcul</b></p>
<p>Pour garantir la sécurité de vos constructions, il est indispensable de connaître les <b><a class="ng-star-inserted" href="https://www.4geniecivil.com/2020/05/quelques-normes-de-calcul-des-elements.html" target="_blank" rel="noopener" data-hveid="0" data-ved="0CAAQ_4QMahcKEwiJkfuV_L6PAxUAAAAAHQAAAAAQXw">normes de calcul des éléments de structure</a></b>. Cette ressource vous fournit un aperçu des réglementations à respecter pour vos projets.</p>
<p>Découvrez cette <a href="https://www.4geniecivil.com/2025/09/note-de-calcul-batiment-detaille-pdf.html">Note de calcul bâtiment</a> détaillé : Guide pratique PDF à télécharger.</p>
<hr />
<h3>Conclusion</h3>
<p class="ds-markdown-paragraph">Le calcul des semelles de fondation est une étape cruciale dans la conception structurelle. Que ce soit pour une semelle ponctuelle ou une semelle linéaire, une approche méthodique garantit la sécurité et la pérennité de l’ouvrage. L’utilisation d’un outil Excel adapté simplifie ce processus et réduit les risques d’erreur.</p>
<hr />
<p class="ds-markdown-paragraph"><strong>Mots-clés</strong> : semelle isolée, semelle continue, calcul fondation, BAEL 91, Excel, note de calcul, contrainte sol, aciers tendus, fissuration, fondation superficielle.</p>
</div>
</div>
</div>
</div>
<div id="ag-popper-container-1756984511880" class="ag-translate-popper-host"> </div>
<p><script src="chrome-extension://lopnbnfpjmgpbppclhclehhgafnifija/aiscripts/script-main.js"></script></p>
<div class="simg-pop-btn" style="top: 180px; left: 14px; display: none;"> </div>
<div class="host-lopnbnfpjmgpbppclhclehhgafnifija" style="position: relative; z-index: 2147483647;"> </div>								</div>
				</div>
					</div>
				</div>
				</div>
		
2 Notes de Calcul de Semelle isolée et semelle filante sur Feuille Excel