<div data-elementor-type="wp-post" data-elementor-id="8229" class="elementor elementor-8229">
				<div class="elementor-element elementor-element-a8372ca e-flex e-con-boxed e-con e-parent" data-id="a8372ca" data-element_type="container">
					<div class="e-con-inner">
				<div class="elementor-element elementor-element-ef74b1d elementor-widget elementor-widget-text-editor" data-id="ef74b1d" data-element_type="widget" data-widget_type="text-editor.default">
				<div class="elementor-widget-container">
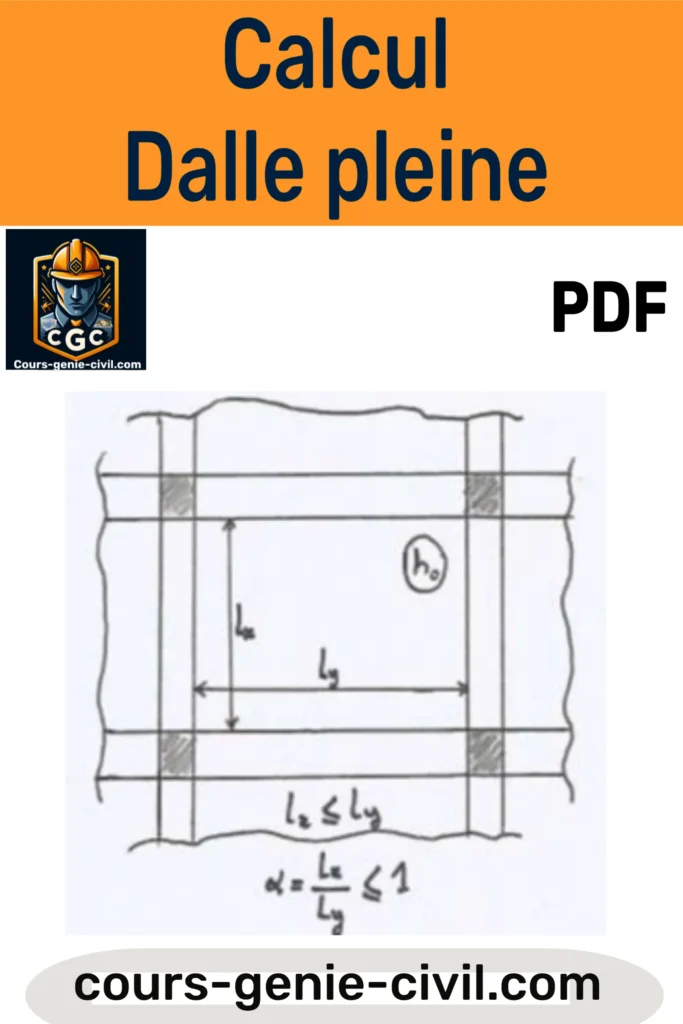
									<p>Cours PDF pour le <strong>Calcul des dalles pleines en béton armé</strong> : méthodes, exemples et conseils pour dimensionner efficacement vos dalles en béton.</p><p><img class="image_Schéma_calcul_dalles_pleines alignnone wp-image-8232 size-large" title="Schéma illustrant le calcul des dalles pleines en béton armé pour une conception structurale" src="https://cours-genie-civil.com/wp-content/uploads/2025/07/Calcul-des-dalles-pleines-en-beton-arme-Cours-PDF-683x1024.webp" alt="Diagramme détaillé illustrant le calcul structurel des dalles pleines en béton armé, avec des armatures, charges et dimensions " width="683" height="1024" /></p><p>Les dalles pleines en béton armé sont des éléments structuraux essentiels dans la construction de bâtiments. Elles servent à répartir les charges du plancher et à transmettre ces forces aux supports (piliers, poutres, murs). Leur conception nécessite une compréhension précise de leurs dimensions, des sollicitations qu’elles doivent supporter, et des méthodes de calcul assurant leur résistance et leur durabilité. Cet article présente une méthode détaillée pour le calcul des dalles pleines en béton armé, en tenant compte des principes fondamentaux de la résistance des matériaux et des règles techniques de construction.</p><hr /><h1>1. Définition et caractéristiques des dalles pleines en béton armé</h1><p>Une dalle pleine est une plateforme horizontale en béton armé, généralement utilisée pour supporter des planchers ou toitures. Elle est caractérisée par ses trois dimensions : la longueur, la largeur, et une hauteur (épaisseur). La hauteur de la dalle est généralement plus petite que ses autres dimensions, ce qui influence ses comportements mécaniques.</p><ul><li><strong>Hauteur (<span class="math math-inline"><span class="katex"><span class="katex-mathml">h</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">h</span></span></span></span></span>)</strong> : épaisseur de la dalle</li><li><strong>Petite portée (<span class="math math-inline"><span class="katex"><span class="katex-mathml">lx</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">l</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">x</span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span>)</strong> : distance entre deux appuis faibles (ou dans un seul sens porteur)</li><li><strong>Grande portée (<span class="math math-inline"><span class="katex"><span class="katex-mathml">ly</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">l</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">y</span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span>)</strong> : distance dans l’autre sens porteur (pour les dalles portées dans deux directions)</li><li><strong>α (<span class="math math-inline"><span class="katex"><span class="katex-mathml">α</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">α</span></span></span></span></span>)</strong> : rapport entre les deux portées, défini par <span class="math math-inline"><span class="katex"><span class="katex-mathml">α=lxly</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">α</span><span class="mrel">=</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">l</span><span class="msupsub"><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">y</span></span><span class="vlist-s">​</span></span></span></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">l</span><span class="msupsub"><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">x</span></span><span class="vlist-s">​</span></span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span></li></ul><hr /><h1>2. Prédimensionnement et cas d’appui</h1><p>Le dimensionnement des dalles dépend de leur mode de portance :</p><ul><li><strong>Portée dans une seule direction</strong> : lorsque <span class="math math-inline"><span class="katex"><span class="katex-mathml">α<;0.4</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">α</span><span class="mrel"><;</span></span><span class="base"><span class="mord">0.4</span></span></span></span></span>, la dalle est portée principalement dans un sens.</li><li><strong>Portée dans deux directions</strong> : lorsque <span class="math math-inline"><span class="katex"><span class="katex-mathml">0.4≤α≤1</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord">0.4</span><span class="mrel">≤</span></span><span class="base"><span class="mord mathnormal">α</span><span class="mrel">≤</span></span><span class="base"><span class="mord">1</span></span></span></span></span>, la dalle supporte dans deux sens.</li></ul><p>La hauteur minimale de la dalle est déterminée en fonction des dimensions et du mode de portée, pour assurer une résistance mécanique suffisante.</p><div class="table-with-header border-grey-line2-normal mb-2 w-fit max-w-full rounded-lg border border-solid"><div class="border-grey-line2-normal flex h-8 items-center justify-between border-0 border-b border-solid px-2 text-xs"><div class="text-text-primary-3 flex items-center gap-1">Table</div><div class="flex gap-1"><div class="text-text-primary-3 hover:text-text-primary-2 flex-center h-[26px] w-[26px] cursor-pointer"> </div></div></div><div class="custom-scrollbar custom-scrollbar-float max-w-full overflow-x-auto"><table class="!mb-0 w-fit !max-w-none"><thead><tr><th>Cas</th><th>Hauteur minimale (<span class="math math-inline"><span class="katex"><span class="katex-mathml">h</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">h</span></span></span></span></span>)</th><th>Expression (en fonction de <span class="math math-inline"><span class="katex"><span class="katex-mathml">lx</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">l</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">x</span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span>)</th></tr></thead><tbody><tr><td>Portée simple (<span class="math math-inline"><span class="katex"><span class="katex-mathml">α<;0.4</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">α</span><span class="mrel"><;</span></span><span class="base"><span class="mord">0.4</span></span></span></span></span>)</td><td><span class="math math-inline"><span class="katex"><span class="katex-mathml">h≥lx22</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">h</span><span class="mrel">≥</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">22</span></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">l</span><span class="msupsub"><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">x</span></span><span class="vlist-s">​</span></span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span> ou <span class="math math-inline"><span class="katex"><span class="katex-mathml">h≥lx25</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">h</span><span class="mrel">≥</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">25</span></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">l</span><span class="msupsub"><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">x</span></span><span class="vlist-s">​</span></span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span></td><td> </td></tr><tr><td>Portée double (<span class="math math-inline"><span class="katex"><span class="katex-mathml">0.4≤α≤1</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord">0.4</span><span class="mrel">≤</span></span><span class="base"><span class="mord mathnormal">α</span><span class="mrel">≤</span></span><span class="base"><span class="mord">1</span></span></span></span></span>)</td><td><span class="math math-inline"><span class="katex"><span class="katex-mathml">h≥lx33</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">h</span><span class="mrel">≥</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">33</span></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">l</span><span class="msupsub"><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">x</span></span><span class="vlist-s">​</span></span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span> ou <span class="math math-inline"><span class="katex"><span class="katex-mathml">h≥lx44</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">h</span><span class="mrel">≥</span></span><span class="base"><span class="mord"><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">44</span></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">l</span><span class="msupsub"><span class="sizing reset-size3 size1 mtight"><span class="mord mathnormal mtight">x</span></span><span class="vlist-s">​</span></span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span></td><td> </td></tr></tbody></table></div></div><hr /><h1>3. Calcul des sollicitations</h1><p>Le dimensionnement repose sur l’analyse des charges et moments fléchissants. Voici un aperçu des principaux éléments :</p><h2>Charges de calcul</h2><ul><li>Charge permanente (poids propre du béton + revêtement)</li><li>Charge d’exploitation (charge utile, poids des matériaux de revêtement)</li><li>Charges accidentelles ou de surcharge selon le contexte</li></ul><h2>Moment de flexion ultime (<span class="math math-inline"><span class="katex"><span class="katex-mathml">Mu</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">M</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">u</span></span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span>)</h2><p>Il se calcule généralement en utilisant des coefficients de sécurité et en tenant compte du type d’appuis et de la configuration de la dalle. Pour une dalle sur 4 appuis, le moment maximal peut s’évaluer à partir de formules standardisées ou de tableaux spécifiques.</p><hr /><h1>4. Vérification de la résistance et armatures</h1><p>Pour assurer la sécurité, il est essentiel de vérifier que la dalle supporte les moments de flexion avec une armature adéquate.</p><h2>Armatures principales</h2><ul><li>Disposition longitudinale pour résister à la flexion</li><li>Calcul de la section d’acier nécessaire (<span class="math math-inline"><span class="katex"><span class="katex-mathml">As</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">A</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">s</span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span>), en fonction du moment maximal</li></ul><h2>Armatures de répartition</h2><ul><li>Posées en dessous de la couche principale pour assurer la ductilité et empêcher la propagation des fissures</li></ul><h2>Disposition constructive</h2><ul><li>Espace entre barres (<span class="math math-inline"><span class="katex"><span class="katex-mathml">St</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord"><span class="mord mathnormal">S</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">t</span></span></span><span class="vlist-s">​</span></span></span></span></span></span></span></span></span>) selon le type de fissuration (peu nuisible, préjudiciable, très préjudiciable)</li></ul><hr /><h1>5. Exemple pratique de calcul</h1><p>Prenons l’exemple d’une dalle de 12 cm d’épaisseur, supportant une charge d’exploitation de 10 kN/m², avec un béton classé <span class="math math-inline"><span class="katex"><span class="katex-mathml">fc28=22</span><span class="katex-html" aria-hidden="true"><span class="base"><span class="mord mathnormal">f</span><span class="mord"><span class="mord mathnormal">c</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist"><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">28</span></span></span><span class="vlist-s">​</span></span></span></span></span><span class="mrel">=</span></span><span class="base"><span class="mord">22</span></span></span></span></span> MPa, et des armatures en acier fe = 400 MPa.</p><ol><li>Calculer la charge de calcul total</li><li>Déterminer le moment fléchissant ultime</li><li>Dimensionner l’armature en accord avec les résultats</li></ol><p>Ce procédé permet d’assurer la conformité des dimensions et des armatures à la norme.</p><hr /><h1>6. Dispositions constructives et fissuration</h1><p>Le choix de l’espacement des barres (St) dépend du mode de fissuration :</p><ul><li>Fissuration peu nuisible : St ≤ min(3h, 33 cm)</li><li>Fissuration préjudiciable : St ≤ min(2h, 25 cm)</li><li>Fissuration très préjudiciable : St ≤ min(1.5h, 20 cm)</li></ul><hr /><h1>7. Conclusion</h1><p>Le dimensionnement précis des dalles pleines en béton armé est une étape cruciale pour garantir leur performance structurelle. En suivant une méthodologie rigoureuse, intégrant la prise en compte des charges, la vérification des moments de flexion, et la disposition optimale des armatures, il est possible de concevoir des dalles sûres, durables et adaptées à leur usage.</p><hr /><h1>Téléchargement du guide complet (PDF)</h1><p>Découvrez notre cours complet en format PDF sur le <strong>Calcul des dalles pleines en béton armé</strong>. Ce guide vous accompagne étape par étape dans la conception, le dimensionnement et le dimensionnement des armatures pour garantir la solidité et la durabilité de vos structures. Qu&rsquo;il s&rsquo;agisse de calculs des charges, du dimensionnement des armatures ou des dispositions constructives, ce cours vous fournit toutes les clés pour réussir vos projets en béton armé. Accédez à des méthodes éprouvées, des exemples concrets et des conseils techniques pour optimiser vos travaux. Que vous soyez étudiant, ingénieur ou professionnel du génie civil, ce <strong>Cours PDF</strong> est une ressource précieuse pour maîtriser facilement le <strong>Calcul des dalles pleines en béton armé</strong> et assurer la sécurité de vos ouvrages.</p><p><span style="font-size: 2em;"><a href="https://cours-genie-civil.com/wp-content/uploads/2025/07/Chapitre-5-Dalles-pleines-beton-arme-1_watermark.pdf" target="_blank" rel="noopener"><b><span style="font-size: xx-large;">ððð</span></b>Télécharger le chapitre complet en PDF</a></span></p><h2>Liens utiles pour approfondir vos connaissances</h2><p>Afin d’approfondir chacun de ces aspects ou de consulter des guides et plans déjà élaborés, voici une sélection de ressources indispensables :</p><ul><li><p><strong>Procédé général de construction en génie civil et guide complet à télécharger en PDF</strong> : pour connaître toutes les étapes et bonnes pratiques dans la réalisation des dalles en béton armé, notamment le dimensionnement, la mise en œuvre, et la vérification structurale. Accéder au <a href="https://cours-genie-civil.com/procedes-generaux-de-construction-en-genie-civil-guide-complet-a-telecharger-en-pdf/" target="_blank" rel="noopener">guide complet de construction en génie civil</a>.</p></li><li><p><strong>Méthodologie détaillée pour le calcul du ferraillage des dalles pleines</strong> : pour une approche précise avec des exemples concrets et le respect des normes. Retrouvez toutes les étapes dans la <a href="https://www.4geniecivil.com/2020/07/calcul-ferraillage-dalle-pleine-pdf.html" target="_blank" rel="noopener">page consacrée au calcul de ferraillage de dalle pleine en PDF</a>.</p></li><li><p><strong>Initiation aux principes fondamentaux des dalles pleines</strong> : pour comprendre les bases et commencer à maîtriser la conception. Consulter cette ressource pour une introduction claire : <a href="https://www.4geniecivil.com/2016/02/initiation-sur-les-dalles-pleines.html" target="_blank" rel="noopener">initiation sur les dalles pleines</a>.</p></li><li><p><strong>Plan de ferraillage de dalle pleine à télécharger en PDF</strong> : pour visualiser des exemples concrets d’armatures et faciliter la conception. Voir le <a href="https://www.4geniecivil.com/2021/12/plan-de-ferraillage-dalle-pleine-pdf.html" target="_blank" rel="noopener">plan de ferraillage</a>.</p></li><li><p><strong>Comment dimensionner une dalle pleine</strong> : pour connaître la méthode étape par étape adaptée à votre projet. La ressource utile est disponible ici : <a href="https://www.4geniecivil.com/2015/08/comment-dimensionner-une-dalle-pleine.html" target="_blank" rel="noopener">comment dimensionner une dalle pleine</a>.</p></li></ul><p>Découvrez aussi le <a href="https://www.4geniecivil.com/2025/07/calcul-des-poutres-en-beton-arme.html" target="_blank" rel="noopener">Calcul des poutres en béton armé</a> : méthode complète &#8211; PDF.</p><p>Trouvez aussi cette <a href="https://cours-genie-civil.com/exercice-corrige-bael-pour-poutre-beton-arme-pdf/">Exercice corrigé BAEL pour poutre</a> béton armé – PDF.</p><p>Voilà aussi ce <a href="https://cours-genie-civil.com/dalle-plaine-guide-complet-pour-concevoir-et-realiser-cette-solution-de-construction/">guide sur la Dalle plaine</a> : concevoir et réaliser cette solution de construction.</p><div id="ag-1752663840150"><p data-start="120" data-end="321">Découvrez le <strong data-start="158" data-end="225"><a href="https://cours-genie-civil.com/tableau-dosage-beton-pdf/">Tableau de dosage béton</a> : proportions par m³ et par sac (35 kg)</strong> avec exemples pratiques, conseils chantier, calculs faciles et <strong data-start="289" data-end="318" data-is-only-node="">PDF gratuit à télécharger</strong>.</p><p data-start="323" data-end="411"> </p></div><p><script src="chrome-extension://lopnbnfpjmgpbppclhclehhgafnifija/aiscripts/script-main.js"></script></p><div id="ag-1753687106379"> </div><div class="host-lopnbnfpjmgpbppclhclehhgafnifija" style="position: relative; z-index: 2147483647;"> </div>								</div>
				</div>
					</div>
				</div>
				</div>
		
Calcul des dalles pleines en béton armé – Cours PDF